En guide til TreeMap i Java
1. Oversikt
I denne artikkelen skal vi utforske TreeMap Implementering av Kart grensesnitt fra Java Collections Framework (JCF).
TreeMap er en kartimplementering som holder oppføringene sortert i henhold til den naturlige rekkefølgen på nøklene, eller enda bedre ved å bruke en komparator hvis den blir levert av brukeren ved konstruksjonstidspunktet.
Tidligere har vi dekket HashMap og LinkedHashMap implementeringer, og vi vil innse at det er ganske mye informasjon om hvordan disse klassene fungerer som ligner.
De nevnte artiklene anbefales sterkt å lese før du går videre med denne.
2. Standard sortering i TreeMap
Som standard, TreeMap sorterer alle oppføringene i henhold til deres naturlige rekkefølge. For et heltall vil dette bety stigende rekkefølge og for strenger, alfabetisk rekkefølge.
La oss se den naturlige rekkefølgen i en test:
@Test offentlig ugyldighet givenTreeMap_whenOrdersEntriesNaturally_thenCorrect () {TreeMap map = new TreeMap (); map.put (3, "val"); map.put (2, "val"); map.put (1, "val"); map.put (5, "val"); map.put (4, "val"); assertEquals ("[1, 2, 3, 4, 5]", map.keySet (). toString ()); }Legg merke til at vi plasserte heltallnøklene på en ikke-ordnet måte, men når du henter nøkkelsettet, bekrefter vi at de faktisk holdes i stigende rekkefølge. Dette er den naturlige rekkefølgen av heltall.
På samme måte, når vi bruker strenger, vil de bli sortert i sin naturlige rekkefølge, dvs. alfabetisk:
@Test offentlig ugyldig givenTreeMap_whenOrdersEntriesNaturally_thenCorrect2 () {TreeMap map = new TreeMap (); map.put ("c", "val"); map.put ("b", "val"); map.put ("a", "val"); map.put ("e", "val"); map.put ("d", "val"); assertEquals ("[a, b, c, d, e]", map.keySet (). toString ()); }TreeMap, i motsetning til et hash-kart og koblet hash-kart, bruker ikke hashing-prinsippet hvor som helst, siden det ikke bruker en matrise til å lagre oppføringene.
3. Egendefinert sortering i TreeMap
Hvis vi ikke er fornøyd med den naturlige bestillingen av TreeMap, kan vi også definere vår egen regel for bestilling ved hjelp av en komparator under konstruksjon av et trekart.
I eksemplet nedenfor vil vi at heltalstastene skal ordnes i synkende rekkefølge:
@Test offentlig ugyldig givenTreeMap_whenOrdersEntriesByComparator_thenCorrect () {TreeMap map = new TreeMap (Comparator.reverseOrder ()); map.put (3, "val"); map.put (2, "val"); map.put (1, "val"); map.put (5, "val"); map.put (4, "val"); assertEquals ("[5, 4, 3, 2, 1]", map.keySet (). toString ()); }Et hash-kart garanterer ikke rekkefølgen på lagrede nøkler og garanterer spesifikt ikke at denne bestillingen vil være den samme over tid, men et trekart garanterer at nøklene alltid blir sortert i henhold til den angitte rekkefølgen.
4. Viktigheten av TreeMap Sortering
Det vet vi nå TreeMap lagrer alle oppføringene i sortert rekkefølge. På grunn av denne egenskapen til trekart kan vi utføre spørsmål som; finn "største", finn "minste", finn alle nøkler mindre enn eller større enn en viss verdi, etc.
Koden nedenfor dekker bare en liten prosentandel av disse tilfellene:
@Test offentlig ugyldig givenTreeMap_whenPerformsQueries_thenCorrect () {TreeMap map = new TreeMap (); map.put (3, "val"); map.put (2, "val"); map.put (1, "val"); map.put (5, "val"); map.put (4, "val"); Heltall høyeste nøkkel = map.lastKey (); Heltall laveste nøkkel = map.firstKey (); Sett keysLessThan3 = map.headMap (3) .keySet (); Sett keysGreaterThanEqTo3 = map.tailMap (3) .keySet (); assertEquals (nytt heltal (5), høyeste nøkkel); assertEquals (nytt heltal (1), laveste nøkkel); assertEquals ("[1, 2]", keysLessThan3.toString ()); assertEquals ("[3, 4, 5]", keysGreaterThanEqTo3.toString ()); }5. Intern implementering av TreeMap
TreeMap redskaper NavigableMap grensesnitt og baserer sitt interne arbeid på prinsippene for rød-svarte trær:
offentlig klasse TreeMap utvider AbstractMap implementerer NavigableMap, Cloneable, java.io.SerializablePrinsippet med rød-svarte trær er utenfor omfanget av denne artikkelen, men det er viktige ting å huske for å forstå hvordan de passer inn i TreeMap.
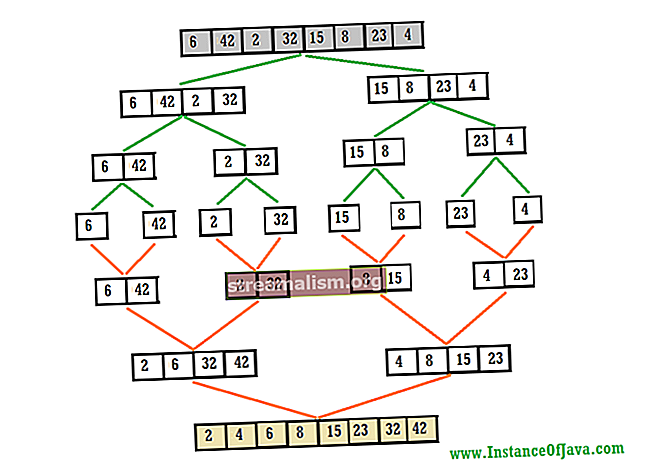
Først av alt, er et rød-svart tre en datastruktur som består av noder; bilde et omvendt mangotre med roten på himmelen og grenene vokser nedover. Roten inneholder det første elementet som er lagt til treet.
Regelen er at startende fra roten er ethvert element i venstre gren av en hvilken som helst node alltid mindre enn elementet i selve noden. De til høyre er alltid større. Hva som definerer større eller mindre enn bestemmes av den naturlige rekkefølgen av elementene eller den definerte komparatoren ved konstruksjon som vi så tidligere.
Denne regelen garanterer at oppføringene til et treemap alltid vil være i sortert og forutsigbar rekkefølge.
for det andre, er et rød-svart tre et selvbalanserende binært søketre. Denne egenskapen og ovennevnte garanterer at grunnleggende operasjoner som å søke, få, sette og fjerne tar logaritmisk tid O (log n).
Å være selvbalanserende er nøkkelen her. Når vi fortsetter å sette inn og slette oppføringer, kan du se treet vokser lenger på den ene kanten eller kortere på den andre.
Dette vil bety at en operasjon vil ta kortere tid på den kortere grenen og lengre tid på grenen som er lengst fra roten, noe vi ikke ønsker å skje.
Derfor blir dette ivaretatt i utformingen av rød-svarte trær. For hver innsetting og sletting holdes den maksimale høyden på treet på en hvilken som helst kant O (log n) dvs. treet balanserer seg kontinuerlig.
Akkurat som hash-kart og koblet hash-kart blir ikke et trekart synkronisert, og derfor er reglene for bruk i et flertrådet miljø de samme som de andre to kartimplementeringene.
6. Velge riktig kart
Etter å ha sett på HashMap og LinkedHashMap implementeringer tidligere og nå TreeMap, er det viktig å lage en kort sammenligning mellom de tre for å veilede oss hvilken som passer hvor.
Et hash-kart er bra som en generell kartimplementering som gir rask lagring og henting. Den kommer imidlertid til kort på grunn av den kaotiske og uordnede ordningen av oppføringer.
Dette får den til å prestere dårlig i scenarier der det er mye iterasjon ettersom hele kapasiteten til den underliggende matrisen påvirker annen traversering enn bare antall oppføringer.
Et lenket hash-kart har de gode egenskapene til hash-kart og legger orden til oppføringene. Det presterer bedre der det er mye iterasjon fordi bare antall oppføringer blir tatt i betraktning uavhengig av kapasitet.
Et trekart tar bestilling til neste nivå ved å gi full kontroll over hvordan nøklene skal sorteres. På baksiden gir det dårligere generell ytelse enn de to andre alternativene.
Vi kan si a koblet hash-kart reduserer kaoset i rekkefølgen av et hash-kart uten å pådra seg ytelsestraff for et trekart.
7. Konklusjon
I denne artikkelen har vi utforsket Java TreeMap klasse og dens interne implementering. Siden det er det siste i en serie vanlige implementeringer av kartgrensesnitt, gikk vi også videre for å kort diskutere hvor det passer best i forhold til de to andre.
Den fullstendige kildekoden for alle eksemplene som brukes i denne artikkelen finner du i GitHub-prosjektet.